Die Form des Tisches und damit alle Übergänge ergeben sich aus einer radialen Symmetrie.
Mit herkömmlichen Programmen erfordert das Finden einer solchen Form einen Kreislauf von:
definierende Kurven ändern, Spiegeln und tangentiale Übergänge wieder neu aufbauen ….
Außerdem sollte das Objekt aus einem Marmorblock gefräst werden, die Übergänge von Fuß zu Platte und Sockel
mussten perfekt sein, da Nachbearbeitung kostspielig wäre.
Lösung:
Die T-Splines Topologie ist so abstrakt angelegt, dass der Designer mit einem Minimum an Vertices/Edges
(gibt’s derer zu viele, wäre die Kontrolle der fließenden Linien äußerst mühsam) einen maximalen Gestaltungsspielraum hat –
aber andererseits detailliert genug, dass die geringen Toleranzen bei Tischplatte und Fuß eingehalten werden können.
Jedes Drehen einer Kante und jedes Ziehen einzelner Vertices zeigt sich unmittelbar auf der radial gespiegelten Seite,
(wobei es immer bei einer zusammenhängen Fläche bleibt – das Problem der Übergänge also entfällt)
was das Entwerfen extrem haptisch macht …
Da der ganze Tisch in einem Stück modelliert wurde, ergaben sich lt. Fräsmeister ideale Fräsbahnen.
Problemstellung:
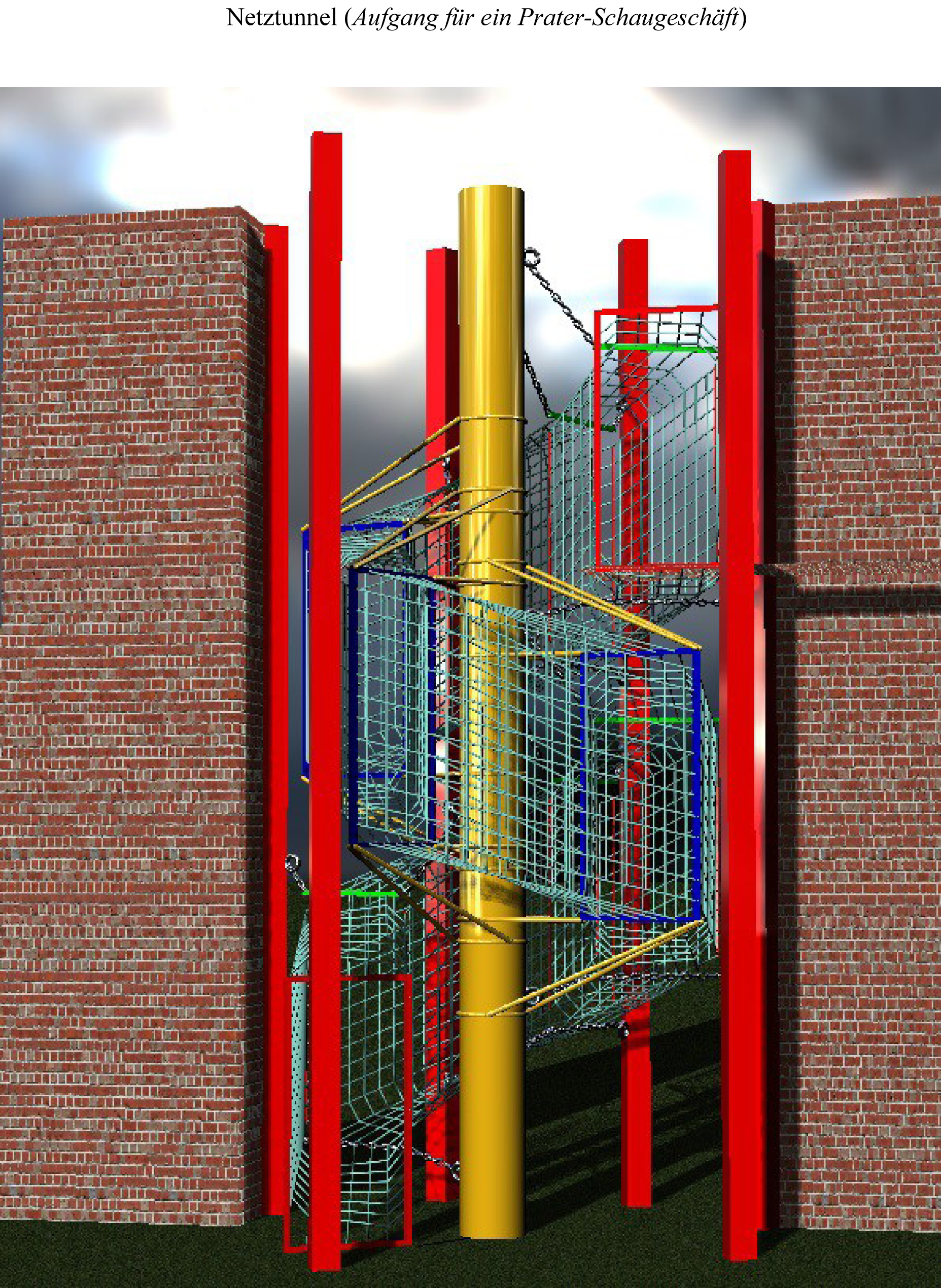
Bei diesem Aufgang zu einem Prater-Schaugeschäft war zu Projektbeginn noch unklar, ob renoviert oder neugebaut werden soll.
Durch die gedrehten Rahmen auf verschiedenen Höhen sollte ein gleichmäßiges Gitternetz geführt werden, das den Sicherheitsnormen (Maschendichte etc.) entsprechen musste.
Da sich der Abstand der Bohrungen auf den Seiten der Profile also aus der Positionierung der Rahmen
(die ja noch nicht festgelegt war) ergibt,
wäre ein Neuzeichen der Konstruktion je Variante – und vor allem des Gitternetzes – ein nicht vertretbarer Aufwand gewesen.
Lösung:
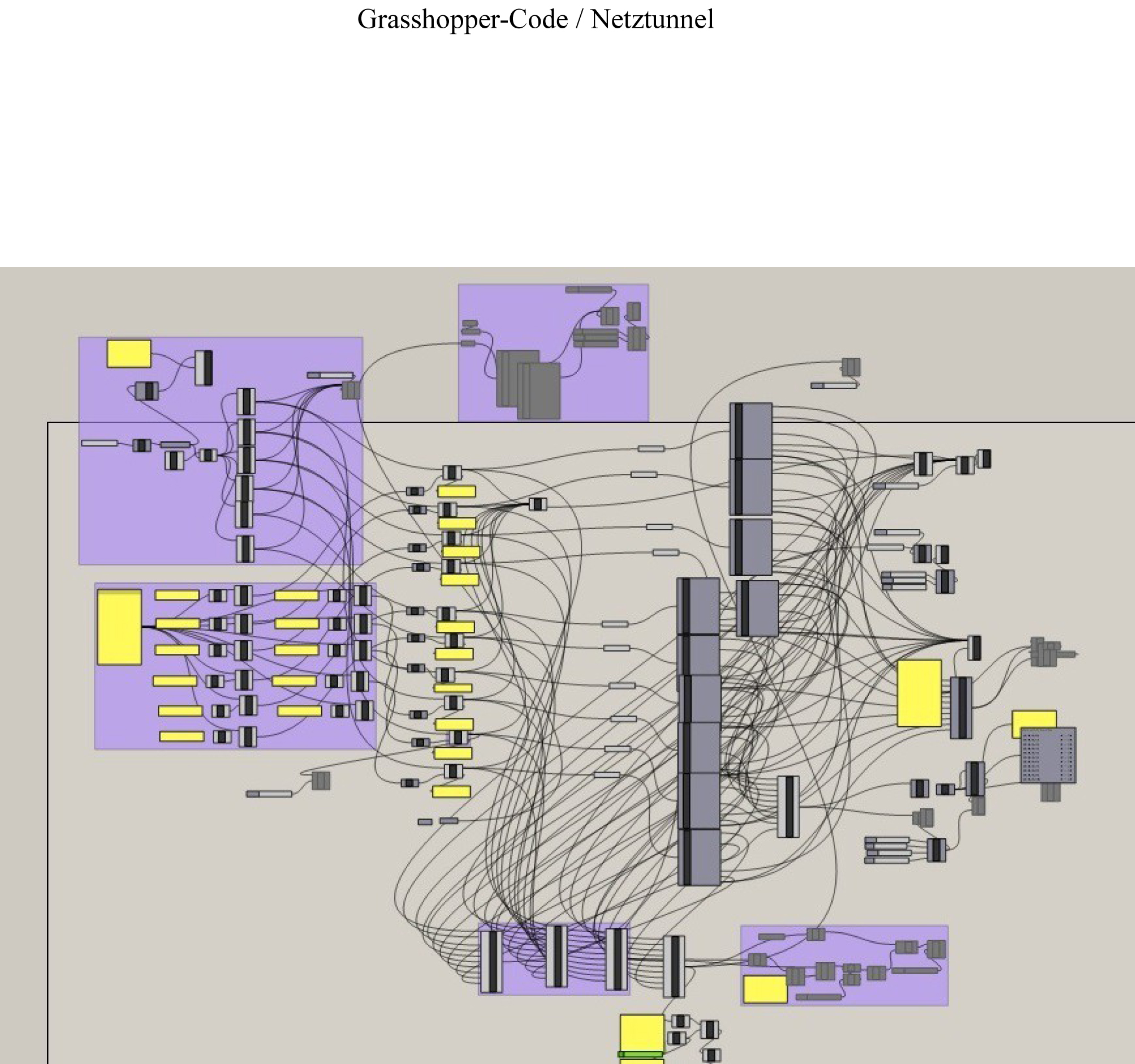
Das Projekt wurde komplett mit Grasshopper programmiert:
Mit jeder Änderung (Anzahl der Steher, Position der Rahmen zueinander etc.)
werden die Bohrungen und damit das komplette Gitternetz neu berechnet.
Im nächsten Bild – zur Veranschaulichung – die oberste Ebene des Grasshopper-Codes:

Auch dieser Ring generiert seine interessante Form aus einer radialen Symmetrie.
Sowohl Anzahl und Dicke der Lamellen (abhängig von Erfordernissen der Gusstechnologie) sowie die Biegung der einzelnen Lamellen (Design) mussten flexibel gehalten werden.
Lösung:
Das T-Splines Modell bot schließlich die Möglichkeit, Verdrehen und Ziehen der Lamellen unter Wahrung dynamisch fließender Konturlinien zu vereinen.
Letzte Anpassungen der Ringschiene wurden in Rhinoceros 3D vorgenommen.
Wiederum erwies sich das „Modellieren in einem Stück“ bei der Fertigung als Vorteil.

Problemstellung:
Angestrebt war eine moderne Interpretation eines 60er-Jahre Möbels,
die Visualisierung sollte auch zur Verständigung bzw. zur Diskussion technischer Fragen mit der Polsterei dienen.
2 Varianten (mit hoher und mit niederer Lehne) waren gewünscht.
Lösung:
Wiederum eine T-Splines-Lösung mit anfänglich einfacher Topologie für’s Entwerfen,
die dann nach und nach für eine realistische Visualisierung verfeinert wurde.

Bei der Ausgestaltung dieses Kindergartens war die Herausforderung, eine Lösung für die Zusammenarbeit einer Designerin, des Kindergarten-Experten und der Professionisten zu finden –
sowie eine haptische Präsentation für die Kindergarten-Pädagogen (ohne 3D-Programme vor Ort) zu finden,
die flexibel auf deren Änderungswünsche eingehen könnte.
Lösung:
Die Projektion der graphischen Entwürfe auf das Interieur wurde mit Rhinoceros 3D und Photoshop realisiert.
Teile der Möblierung (z.b. die Rutsche von einem Fremdhersteller) wurden mit T-Splines modelliert.
Als Kommunikations- und Präsentationstool hat sich eine Visualisierung als als 3D-PDF bewährt.

Geplant war eine Serie von Ringen basierend auf zu verschiedenen Steinformen passenden Polygonen.
Dabei sollte eine einheitliche Produktlinie erkennbar werden, diese würde sich durch die wechselseitige
Anpassung des 3-, 5- und 7-eckigen Ringes entwickeln, d.h. :
auch hier war wieder maximale Flexibilität gefragt.
Lösung:
Die T-Splines für die verschiedenen Ringtypen hatten zwar eine unterschiedliche Topologie,
ließen sich aber formal leicht aufeinander abstimmen
Von Vorteil war dabei auch das gestalterische Potential und die Flexibilität von T-Splines
bei den Übergängen von Ringkopf zur Ringschiene und bei den Verrundungen für die Gussformen.